Aljabar Boolean & Boolean Logic

Aljabar Boolean 

Aljabar Boolean atau dalam bahasa Inggris disebut dengan Boolean Algebra adalah matematika yang digunakan untuk menganalisis dan menyederhanakan Gerbang Logika pada Rangkaian-rangkaian Digital Elektronika. Boolean pada dasarnya merupakan Tipe data yang hanya terdiri dari dua nilai yaitu “True” dan “False” atau “Tinggi” dan “Rendah” yang biasanya dilambangkan dengan angka “1” dan “0” pada Gerbang Logika ataupun bahasa pemrograman komputer. Aljabar Boolean ini pertama kali diperkenalkan oleh seorang Matematikawan yang berasal dari Inggris pada tahun 1854. Nama Boolean sendiri diambil dari nama penemunya yaitu George Boole.

Hukum Aljabar Boolean

Dengan menggunakan Hukum Aljabar Boolean ini, kita dapat mengurangi dan menyederhanakan Ekspresi Boolean yang kompleks sehingga dapat mengurangi jumlah Gerbang Logika yang diperlukan dalam sebuah rangkaian Digital Elektronika.

Dibawah ini terdapat 6 tipe Hukum yang berkaitan dengan Hukum Aljabar Boolean

Hukum Komutatif (Commutative Law)

Hukum Komutatif menyatakan bahwa penukaran urutan variabel atau sinyal Input tidak akan berpengaruh terhadap Output Rangkaian Logika.

Contoh :

Perkalian (Gerbang Logika AND)

X.Y = Y.X

Penjumlahan (Gerbang Logika OR)

X+Y = Y+X

Catatan : Pada penjumlahan dan perkalian, kita dapat menukarkan posisi variabel atau dalam hal ini adalah sinyal Input, hasilnya akan tetap sama atau tidak akan mengubah keluarannya.

Hukum Asosiatif (Associative Law)

Hukum Asosiatif menyatakan bahwa urutan operasi logika tidak akan berpengaruh terhadap Output Rangkaian Logika.

Contoh :

Perkalian (Gerbang Logika AND)

W . (X . Y) = (W . X) . Y

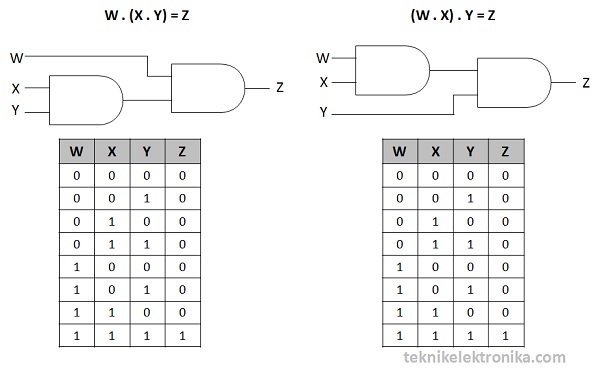
Penjumlahan (Gerbang Logika OR)

W + (X + Y) = (W + X) + Y

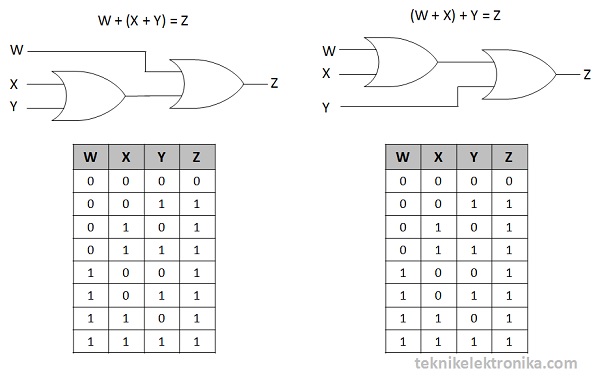
Catatan : Pada penjumlahan dan perkalian, kita dapat mengelompokan posisi variabel dalam hal ini adalah urutan operasi logikanya, hasilnya akan tetap sama atau tidak akan mengubah keluarannya. Tidak peduli yang mana dihitung terlebih dahulu, hasilnya tetap akan sama. Tanda kurung hanya sekedar untuk mempermudah mengingat yang mana akan dihitung terlebih dahulu.

Hukum Distributif

Hukum Distributif menyatakan bahwa variabel-variabel atau sinyal Input dapat disebarkan tempatnya atau diubah urutan sinyalnya, perubahan tersebut tidak akan mempengaruhi Output Keluarannya.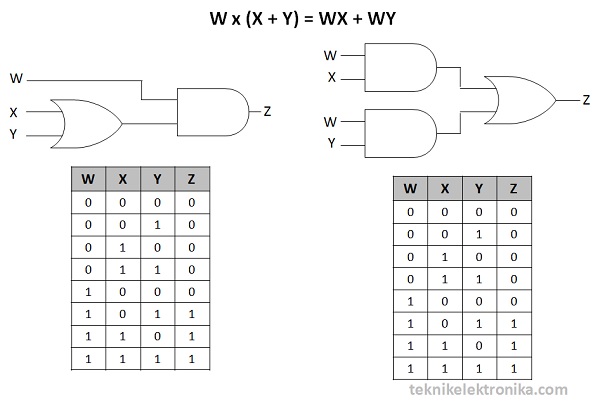

Hukum AND (AND Law)

Disebut dengan Hukum AND karena pada hukum ini menggunakan Operasi Logika AND atau perkalian. Berikut ini contohnya :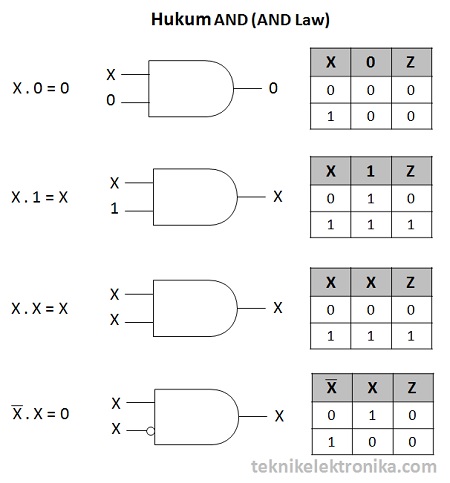

Hukum OR (OR Law)

Hukum OR menggunakn Operasi Logika OR atau Penjumlahan. Berikut ini adalah Contohnya :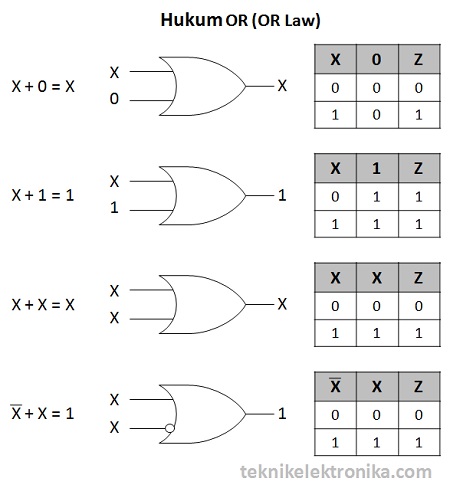

Hukum Inversi (Inversion Law)

Hukum Inversi menggunakan Operasi Logika NOT. Hukum Inversi ini menyatakan jika terjadi Inversi ganda (kebalikan 2 kali) maka hasilnya akan kembali ke nilai aslinya.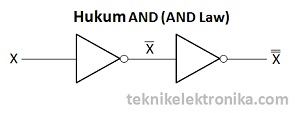

Jadi, jika suatu Input (masukan) diinversi (dibalik) maka hasilnya akan berlawanan. Namun jika diinversi sekali lagi, hasilnya akan kembali ke semula.

Boolean Logic

Boolean Logic, dikembangkan oleh George Boole (1815-1864), sering digunakan untuk menyaring penetapan suatu status sistem atau untuk men-set bit atau meng-clear bit. Boolean logic itu salah satu cara sederhana membandingkan bit-bit individual. ini digunakan oleh yang namanya operators untuk menentukan bagaimana bit-bit itu dibandingkan. mereka mensimulasikan gerbang-gerbang yang akan anda lihat di bagian hardware nanti.(ga tau nantinya kapan :)).

Contoh dibawah ini hanya akan menunjukkan 2 input dan 1 output untuk setiap gerbang, walaupun gerbang-gerbang bisa lebih dari itu. gerbang-gerbang logika juga sering dikombinasikan pada bentuk2 logic yang lebih kompleks. suatu mikroprosesor modern dapat mengandung angka-angka besar dengan banyak input dan banyak kombinasi-kombinasi yang bervariasi. untuk catatan, istilah on,high, dan 1 akan dianggap sebagai keadaan logika yang sama, serta off,low, dan 0 merupakan keadaan logika yang sama.

Jenis - jenis Gerbang Logika

Terdapat 7 jenis Gerbang Logika Dasar yang membentuk sebuah Sistem Elektronika Digital, yaitu :

Gerbang AND
Gerbang OR
Gerbang NOT
Gerbang NAND
Gerbang NOR
Gerbang X-OR (Exclusive OR)
Gerbang X-NOR (Exlusive NOR)

Gerbang AND

Dimana jika hanya semua inputnya on, maka oiutputnya akan on. jika salah satu inputnya off, maka outputnya akan off. akan mudah melihat semua kombinasi input2 dengan menggunakan tabel kebenaran seperti dibawah ini.

(disetiap bagian bawah tabel terdapat simbol gerbang logikanya)

AND (all high = high, else low)

Input 1  Input 2  Output

0              0              0

0              1              0

1              0              0

1              1              1

Control And Embedded Systems

Gerbang OR

sedangkan operasi OR itu kalo salah satu inputnya on, maka outputnya akan on. berikut tabel kebenarannya

OR (any high = high, else low)

Input 1  Input 2  Output

0              0              0

0              1              1

1              0              1

1              1              1

Control And Embedded Systems

Ada 2 operasi logika yang sama seperti diatas, tapi dengan output yang di-NOT-kan (inverted output), yaitu NAND dan NOR.

Gerbang NAND(Not AND) 

Jika dan hanya jika semua inputnya on, maka outputnya akan off , dan jika salah satu inputnya off, maka outputnya akan on (kebalikannya dari operasi AND). dan inilah tabel kebenarannya :

NAND (all high = low, else high)

Input 1  Input 2  Output

0              0              1

0              1              1

1              0              1

1              1              0

Control And Embedded Systems

Gerbang NOR

Sedangkan operasi NOR itu jika salah satu inputnya on, maka outputnya akan off (kebalikannya dari OR). Lihat tabel kebenaran :

NOR (any high = low, else high)

Input 1  Input 2  Output

0              0              1

0              1              0

1              0              0

1              1              0

Control And Embedded Systems

Gerbang XOR

Untuk operasi OR, ada variasi operasi yang disebut Exclusive OR atau XOR. operasi ini akan mempunyai output on jika input-inputnya berbeda. lihat aja tabel kebenarannya dibawah ini :

XOR (different = high, same = low)

Input 1  Input 2  Output

0              0              0

0              1              1

1              0              1

1              1              0

Control And Embedded Systems

Gerbang NOT

Ada satu lagi, operasi INVERTER atau NOT, yang hanya mempunyai satu input, dimana outputnya merupakan kebalikan dari inputnya. contohnya jika inputnya berlogik 1, maka outputnya akan berlogik 0. lihatlah tabel kebenarannya :

NOT (inverter)

Input = 1              Output = 0

Input = 0              Output = 1

Control And Embedded Systems

Sumber : 

http://baguzerror88.blogspot.com/2009/08/boolean-logic.html
https://ernantodwi0112.blogspot.com/2018/12/aljabar-bolean.html?m=1
https://teknikelektronika.com/pengertian-aljabar-boolean-hukum-aljabar-boolean/